线性分类器
图像表示
将图像转换成向量的方法有很多,最直接的方法是将图像矩阵转换成向量
图像类型
- 二进制图像(非黑即白)
- 灰度图像(一个像素由一个bit表示,取值范围0~255;图像的像素取值范围都是0~255,最黑是0,最白是255)
- 彩色图像(每个像素点有3个值,即有3个bit,分别记录R、G、B)
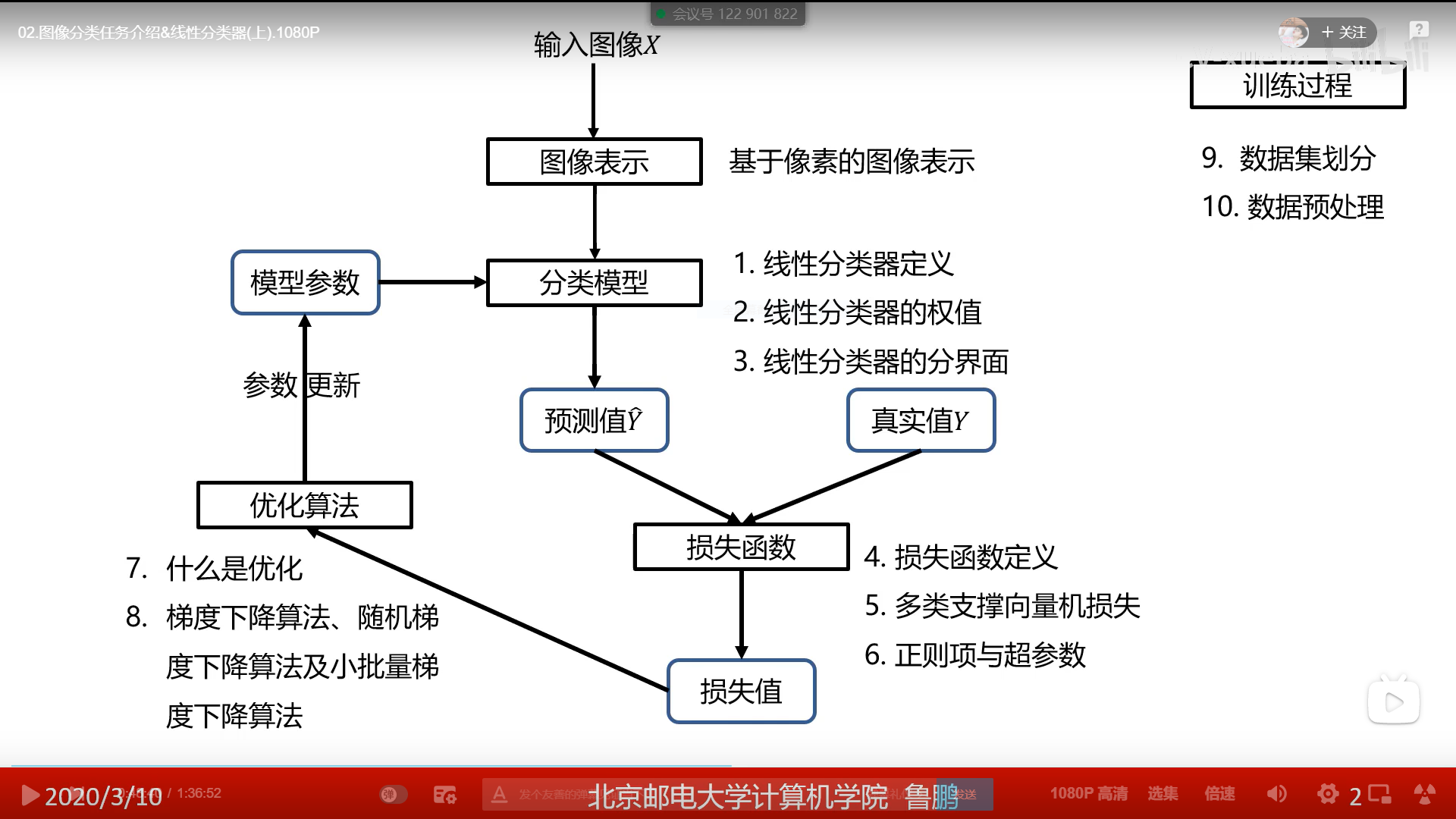
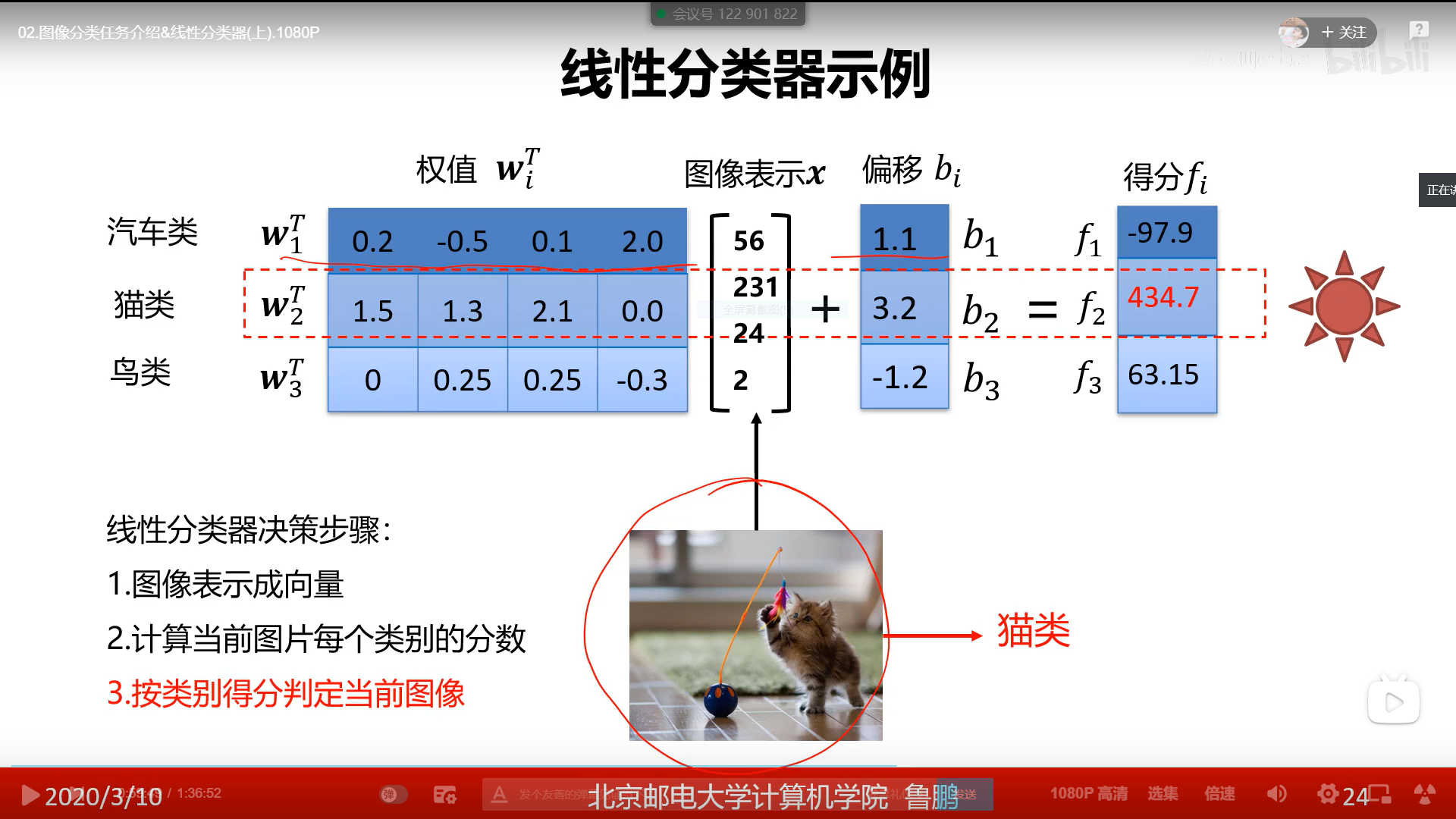
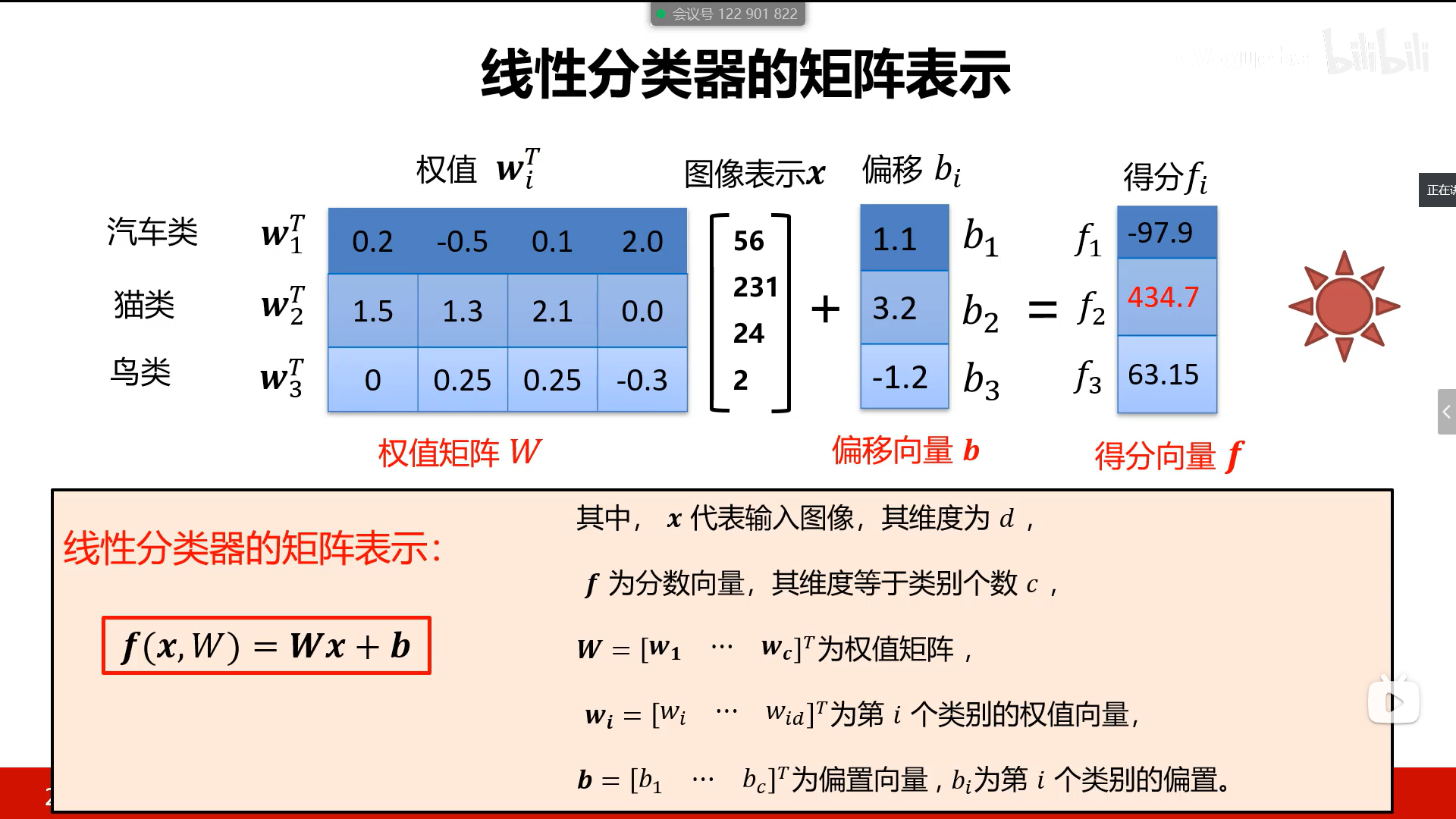
线性分类器
- 线性分类器是一种线性映射,将输入的图像特征映射为类别分数
- 有n类图像就有n个w,b,即每类图像都有自己的w,b
- 把图片放入得到n个分数,分数最大的即为结果
为什么从线性分类器开始
- 形状简单,易于理解
- 通过层级结构(神经网络)或则高维映射(支持向量机)可以形成功能强大的非线性模型
线性分类器的权值
把w放入一个32 32 3的矩阵中,把其中的值规划到0~255之间,生成的图片和目标图片很相似;w记录了该类别信息的平均值,当物体和w越像的时候,他们之间的点乘值就是一个很大的值。
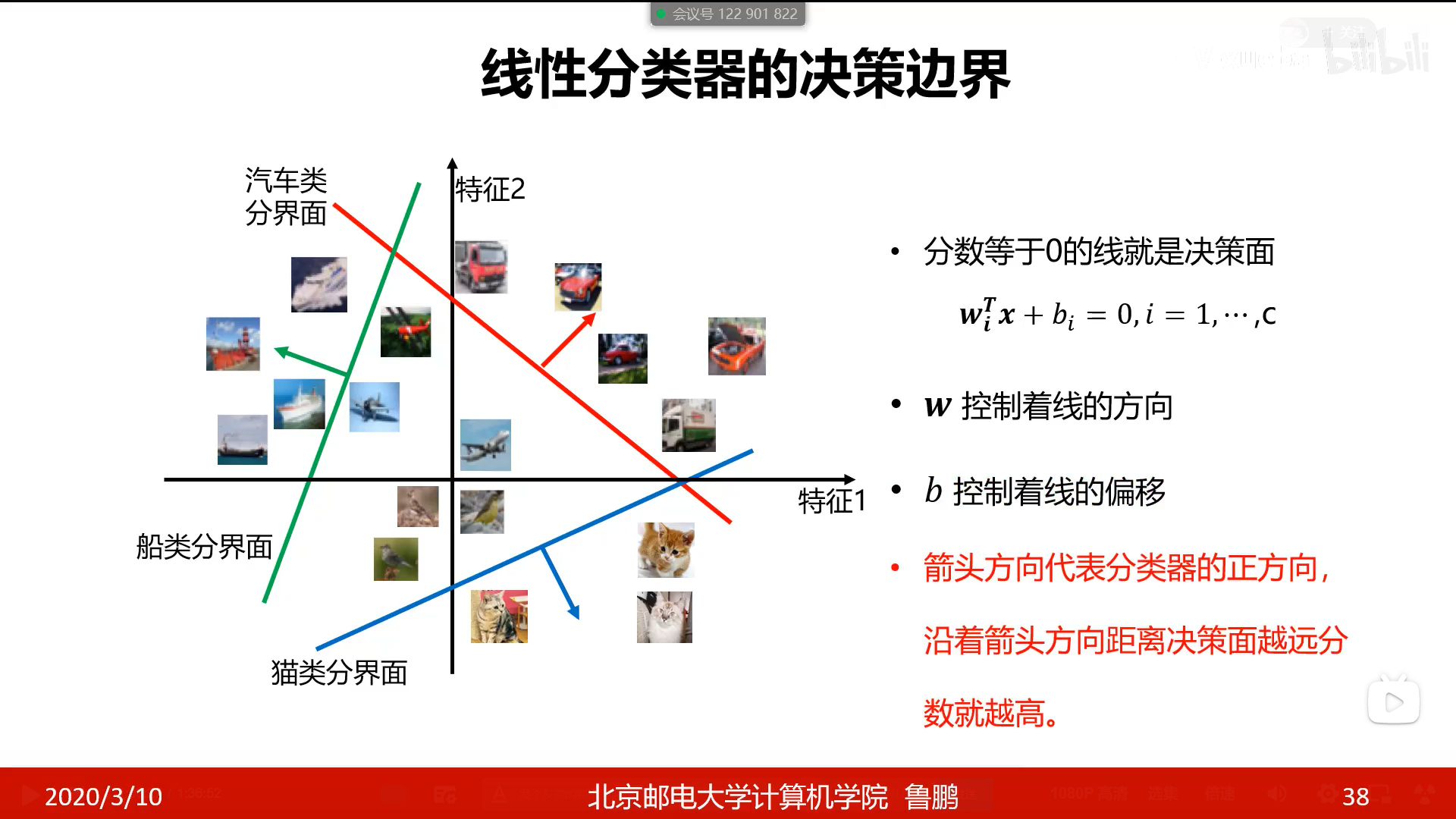
线性分类器的分界面
- 分数等于0的面试决策面
- 在分界面的正方向,离分界面越远正确率越高(或把x代入wx+b中,得分越高正确率越高)
当判断分类器的分类效果时,需要损失函数来帮忙
损失函数
损失函数搭建了模型性能与模型参数之间的桥梁,指导模型参数优化。
- 损失函数是一个函数,用于度量给定分类器的预测值与真实值的不一致程度,其输出通常是一个非负实数
- 其输出的非负实数值可以作为反馈信号来对分类器参数进行调整,以降低当前示例对应的损失值,提升分类器的分类效果
- 损失为平均损失
多类支持向量机损失
用n个w,b对同一样本进行预测得到n个数,把wi,bi预测出的syi除外,拿syi与其他预测值比较,若syi比其他测试值大1,则损失函数为0,否则通过上图公式进行计算;
1为限定的边界值,一般取1;
问题抢答
- 最小是0;最大可能是正无穷;
- 损失L可能是n-1,即分类数-1;因为当w,b非常接近于0时,Li的值为n-1,有n个n-1,则L近似为n-1;
- Li的值会+1,对训练结果没有影响;
- 可以代替,因为求和是平均n的倍数,损失大的还是大,损失小的还是小;
- 使用平方会可能会对训练结果产生影响;
正则项和超参数
问题:假设存在一个w使损失函数为0,这个w是唯一的吗?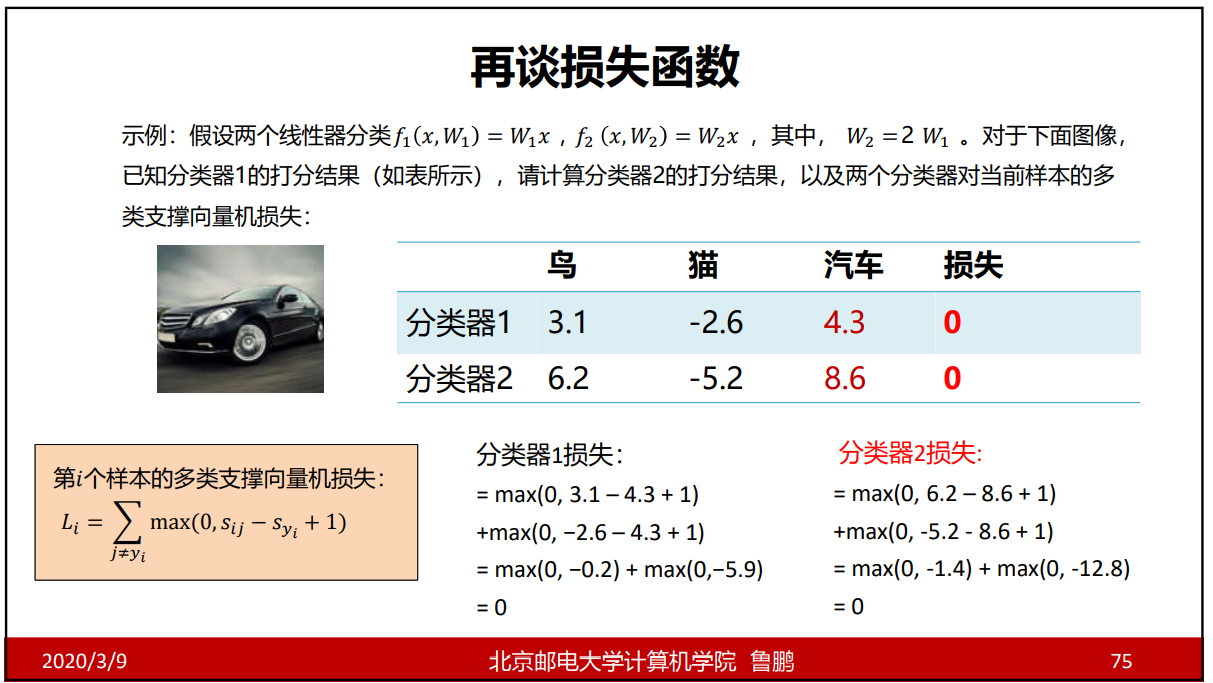

这个时候就引入了正则项。
正则项

正则项的三个作用
- 让解唯一
- 让模型有了偏好
- 抵抗过拟合(防止只在训练集在学习的太好)
常用的正则项损失函数
Elastic net(L1+L2)是弹性网络正则,即L1和L2组合起来的。
超参数
是在训练之前自己设置的,而不是在训练过程中学习优化得到的。
什么是参数优
参数优化
参数优化是利用损失函数的输出值作为反馈信号来调整分类器参数,以提升分类器对训练样本的预测能力。
优化目标
损失函数L是一个与参数w有关的函数,优化的目标就是找到损失函数L达到最优的那组w。
梯度下降算法
梯度下降算法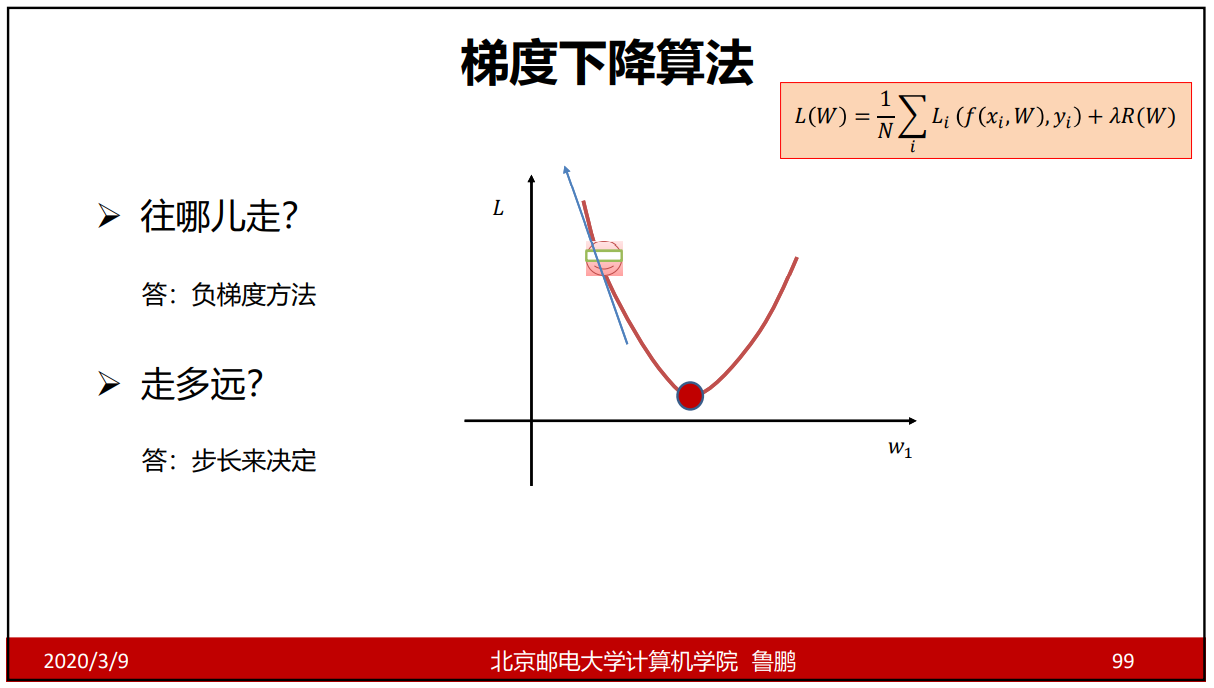

梯度下降算法的下降过程如L,w坐标图所示,我们可以理解任意一个w都对应一个L,我们从模型上的任意一点开始,若它在单调递减区间,那么它在这一点的梯度方向是向左上的,且导数为负数,因为我们要向负梯度方向移动,即向右下方向,此时随着w的增加L值减小;同理当L在单调增区间时,梯度的值为正,则L随着w的不断减少而减少。
更新权值的计算公式:新权值 = 老权值 - 学习率(步长) * 权值的梯度;
梯度计算方法的比较


数值梯度:近似,慢,易写
解析梯度:精确,快,易错
数值梯度的作用:求梯度时一般是用的是解析梯度,而数值梯度主要用于解析梯度正确性的校验(梯度检查);若两者的计算结果非常接近,则说明在这部分代码从应该没有问题。

采用梯度下降法,是把所有的样本计算一次才更新一次w,计算量较大,且效率较低。
随机梯度下降法

方法1:有一百万个样本,算完了一百万个样本更新一次w,更新一百万次w;
方法2:有一百万个样本,每个样本更新一次,更新一百万次w;
那么方法2肯定比方法1好,起码速度上比较快,精确上也接近;
因此,在样本N很大时,权值的梯度计算量很大,下降很慢,改进方法就是采用随机梯度下降法,因为每次只采用有一个样本,梯度更新会更快。
但是就会出现问题:如果有些样本是噪声,那梯度方向会不会沿着反方向走?
随机梯度下降法是每次随机挑选一个样本去更新w,虽然单个样本可能使L向增大的方向走,但大部分样本会让我们整体是一个往下走的方式。
小批量梯度下降算法

epoch:1个epoch表示用过了一个训练集中的所有样本(并不是所有样本都用过了,而是所用的样本总数达到了N);
100次迭代每次用100个样本和1000次迭代每次用10个样本,这两则对样本的利用率是一样的;
梯度下降算法总结

数据集划分

训练集用于对参数的训练,当模型中有超参数时,通过验证集把超参数给选择出来,并通过测试集去测试模型的泛化能力;当对参数和超参数确定的过程中,测试集对模型是不可见的。
当数据太少,那么验证集所包含的样本就很少,从而无法统计上代表的数据
K折验证和重复的K折验证
举例:在区分男女的模型中,拿10%的数据作为验证集,且这部分数据都是女生;模型1对男女的区别的正确率都是90%,模型2对男生的正确区分率是0%,对女生的正确区分率是100%;那么结果就会表现出模型2是优秀的,但实际上并不是。
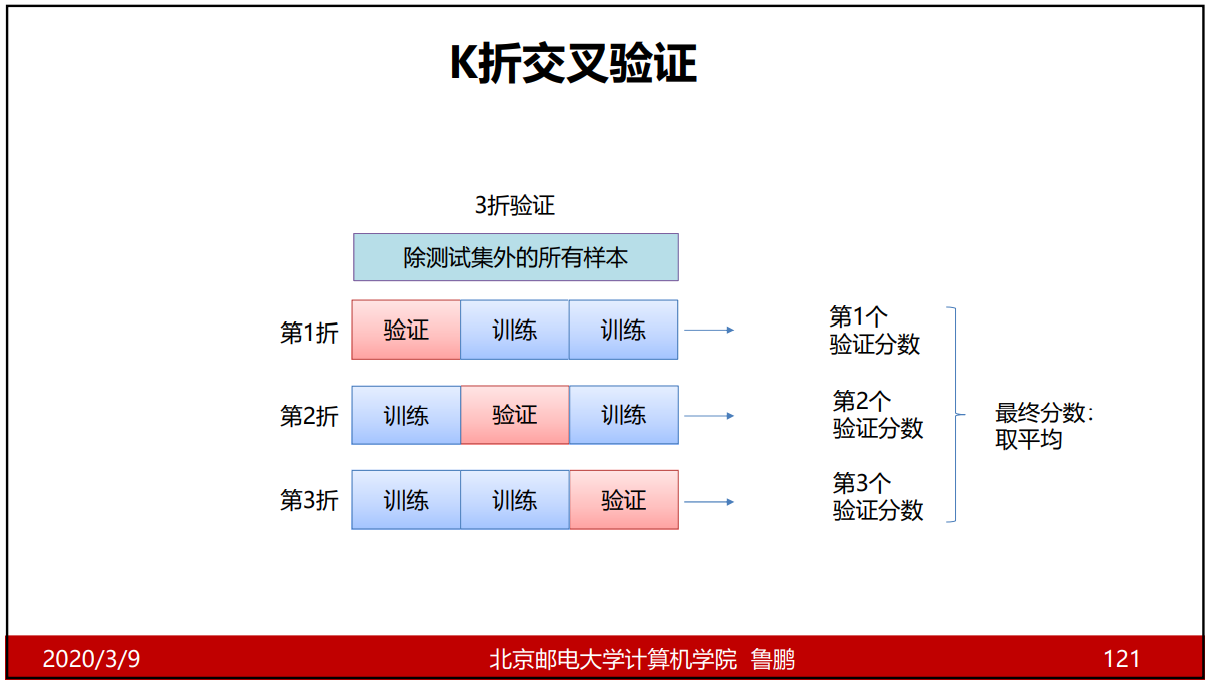
K折验证
重复的K折验证
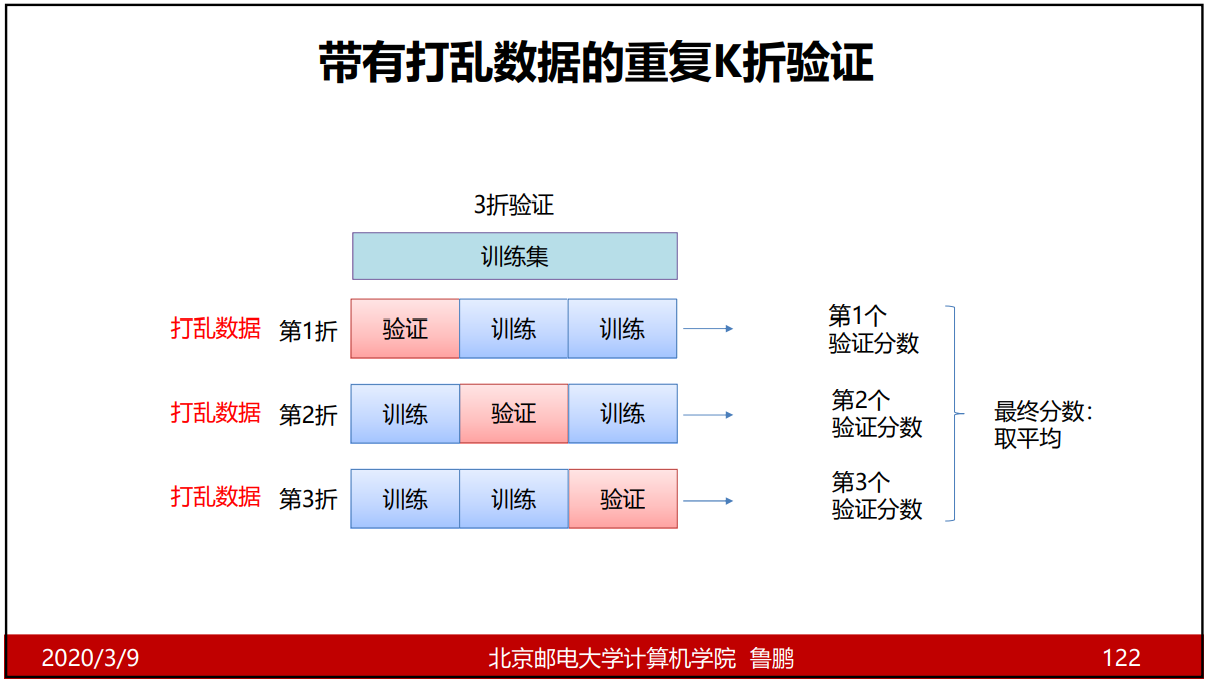
K就是分的块数,常用5折和10折;当大量数据时,一般取5%作为验证集,则不再做交叉验证。
数据预处理
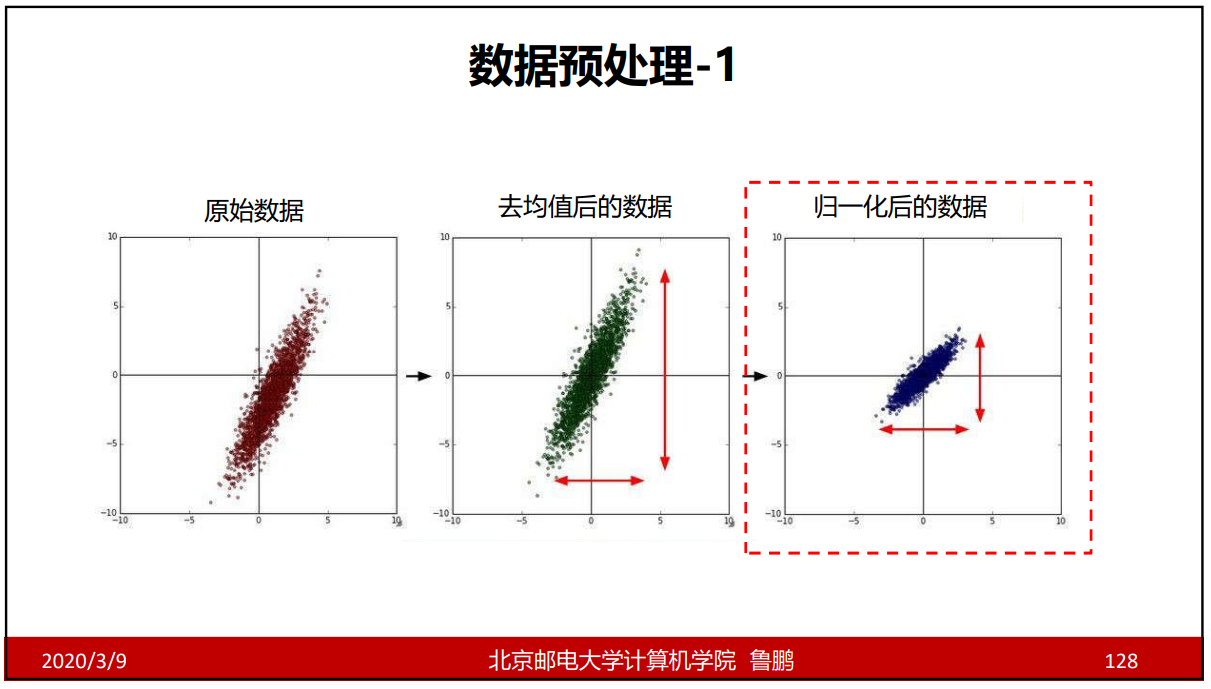
去均值后的数据:去均值就是把数据归到中心来,训练数据时看的是相对差值而不是绝对差值,保证数据不会受到数据范围的影响。
归一化后的数据:保证数据不会受到量纲的影响。
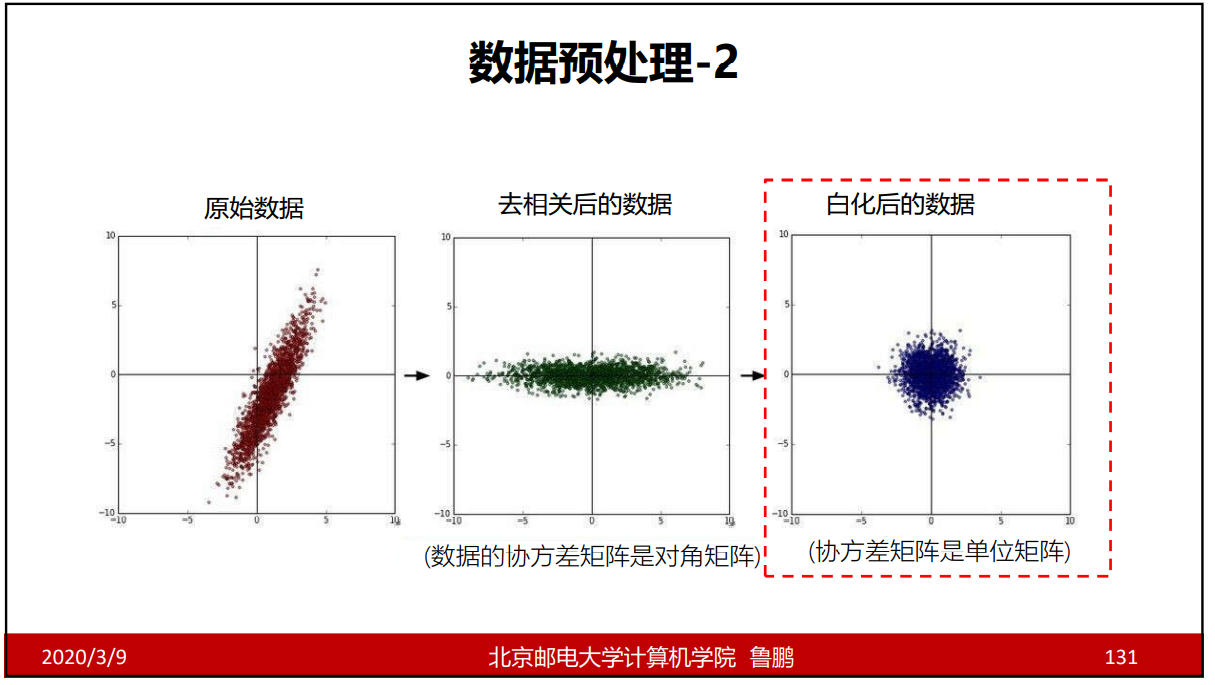
去相关:让数据独立出来;能尽量减少某些在维度上没有变化的数据,这些数据就不考虑了;